
<span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">Python en ciencias e ingeniería: tutoriales basados en ejemplos</span> por <span xmlns:cc="http://creativecommons.org/ns#" property="cc:attributionName">Sergio Gutiérrez Rodrigo y Adrián Navas Montilla</span> se distribuye bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional.
Introducción: cálculo vectorial utilizando Jupyter Notebook ¶
Esto es un cuaderno interactivo donde podemos añadir celdas de texto (como esta), o celdas de código (como la celda inferior). Las celdas de texto permiten escribir texto con distintos formatos y ecuaciones como esta: $$c=a·b$$ Para editar una celda de texto basta con hacer doble click en ella. Las celdas de código permiten ejecutar código en lenguaje Python, por ejemplo, podemos asignar valores a las variables $a$ y $b$ de la fórmula anterior y calcular $c$, como si de una calculadora de tratara:
a= 2.0
b= 3.0
c=a*b
print("El resultado de a*b es:",c) #la función print() permite mostrar
#por pantalla texto y variables numéricas o simbólicas
Lo primero que debemos hacer es cargar las librerías necesarias de Python. Como vamos a trabajar con cálculo simbólico y numérico cargaremos las librerías sympy y numpy. Además, para hacer representaciones gráficas cargaremos la librería matplotlib. En la siguiente celda de código se cargan estas librerías:
from sympy import * # Librería para trabajo simbólico
import numpy as np # Librería para cálculo numérico
import math # Librería para utilizar símbolos matemáticos
# como el número pi, que se escribe como math.pi
import matplotlib.pyplot as plt # Librería para poder dibujar gráficas
from IPython.display import display
Aprendiendo a trabajar con vectores¶
Para definir un vector utilizaremos el comando Matrix(). Vamos a definir dos vectores $\vec{\mathbf{u}}=(1,2,0)$ y $\vec{\mathbf{v}}=(3,3,1)$ de 3 componentes:
u=Matrix([[1,2,0]])
v=Matrix([[3,3,1]])
print("El vector u es:")
display(u)
print("Sus componentes son:",u[0],u[1],u[2])
print("\nEl vector v es:")
display(v)
print("Sus componentes son:",v[0],v[1],v[2])
Podemos realizar facilmente el producto escalar entre ellos:
$$w=\vec{\mathbf{u}}\cdot\vec{\mathbf{v}}=(u_1,u_2,u_3)·\left(\begin{array}{c} v_1\\ v_2\\ v_3 \end{array} \right)=u_1v_1+u_2v_2+u_3v_3=1·3+2·3+0·3=9$$de la siguiente manera:
w=u.dot(v) #significa u multiplicado escalarmente por v
print("El producto escalar es:")
print(w)
import numpy as np
u2=np.array(u)
v2=np.array(v)
v2=np.reshape(v2,(3,1))
print(u2.shape,v2.shape)
w2=u2@v2
print("El producto escalar es:")
print(w2)
Observando que el producto vectorial da como resultado un escalar, ya que:
$$w=\vec{\mathbf{u}}\cdot\vec{\mathbf{v}}= |\vec{\mathbf{u}}| |\vec{\mathbf{v}}| \cos \theta$$donde $\theta$ es el ángulo entre los vectores.
También podemos calcular el producto vectorial
$$\vec{\mathbf{w}}=\vec{\mathbf{u}}\times\vec{\mathbf{v}}=\left( \begin{array}{c} u_2v_3-v_2u_3\\ v_1u_3-u_1v_3\\ u_1v_2-v_1u_2 \end{array} \right)=\left( \begin{array}{c} 2·1-3·0\\ 3·0-1·1\\ 1·3-3·2 \end{array} \right) $$de la siguiente manera:
w=u.cross(v) #significa u multiplicado vectorialmente por v
print("El producto vectorial es:")
display(w)
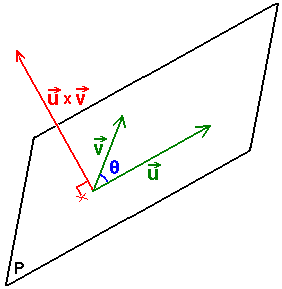
Observando que el producto vectorial da como resultado un vector. Recordad que la dirección de $\vec{\mathbf{w}}$ será la del vector ortogonal a los vectores $\vec{\mathbf{u}}$ y $\vec{\mathbf{v}}$ según la regla de la mano derecha:
Introducción al cálculo diferencial con funciones de varias variables: gradiente¶
En este apartado vamos a aprender a definir funciones, calcular sus derivadas, etc. Consideremos la siguiente función correspondiente a un campo escalar de potencial electrostático en 2 dimensiones:
$$ ϕ(x,y) = x^2 + y^2 + 10 $$Las variables $x$ e $y$ de las que depende la función debemos declararlas como variables simbólicas, ya que todavía no les hemos asignado un valor numérico
x,y=symbols('x y') #Declaramos x e y como variable simbólica:
#nos permite "arrastrarla" como un símbolo hasta que decidamos darle valor.
Para definir la función $\phi(x,y)$ haremos lo siguiente:
def phi(x,y):
return x**2+y**2+10
Y para evaluarla en un punto (p. ej en $x=1.7$ y $y=1.5$), podemos hacerlo de dos maneras distintas:
#Opcion 1
print(phi(1.7,1.5))
#Opcion 2
print(phi(x,y).subs([(x,1.7),(y,1.5)]))
Antes de continuar, vamos a hacer una representación gráfica de esta función en el dominio espacial $[0,2]\times[0,2]$
L=2 #longitud del dominio
N = 100 #espaciado entre puntos
xp = np.linspace(0, L, N) #puntos en x
yp = np.linspace(0, L, N) #puntos en y
X, Y = np.meshgrid(xp, yp) #matriz de puntos
Z = phi(X,Y) #valores de phi(x,y) en los puntos
fig, ax = plt.subplots() #genera el objeto "figura"
CS = ax.contourf(X, Y, Z) #hace la representación gráfica
#Esto es para configurar ejes, barra de color, etiquetas, etc...
ax.clabel(CS, inline=True, fontsize=10, colors='black')
ax.set_title('Potencial $\phi(x,y)$')
ax.set_xlabel("x")
ax.set_ylabel("y")
fig.colorbar(CS)
También podemos hacer gráficas en una dimensión (más sencillas). Por ejemplo, podemos representar $\phi(x,y)$ a lo largo del eje $x$ (es decir, haciendo $y=0$):
L=2 #longitud del dominio
N = 100 #espaciado entre puntos
xp = np.linspace(0, L, N) #puntos en x
pot = phi(xp,0.0)
fig, ax = plt.subplots() #genera el objeto "figura"
ax.plot(xp,pot) #pinta la gráfica
ax.set_xlabel("x")
ax.set_ylabel("$\phi(x,0)$")
Gradiente¶
Ahora vamos a aprender a calcular una derivada parcial de una función. En este caso calcularemos las derivadas parciales de $\phi(x,y)$ respecto de $x$ e $y$:
$$\frac{\partial \phi(x,y)}{\partial x} \hbox{ y } \frac{\partial \phi(x,y)}{\partial y}$$para ello, utilizamos el método diff() :
dphidx = phi(x,y).diff(x) #calcula la derivada parcial respecto a x
dphidy = phi(x,y).diff(y) #calcula la derivada parcial respecto a y
print('La derivada de $\phi$ respecto de x es=',dphidx)
print("La derivada de $\phi$ respecto de y es =",dphidy)
Dado que $\phi(x,y)$ es un campo escalar en dos dimensiones, es muy útil el uso del gradiente para calcular variaciones en el plano $x,y$ y direcciones de máxima variación. El gradiente de $\phi(x,y)$ es un vector en cuyas componentes tenemos las derivadas de $\phi$ respecto de las distintas coordenadas espaciales:
$$\nabla \phi(x,y)=\left(\begin{array}{c} \frac{\partial \phi(x,y)}{\partial x}\\ \frac{\partial \phi(x,y)}{\partial y} \end{array} \right)$$donde $\nabla$ es el operador nabla. Vamos a construir el gradiente de $\phi$:
gradphi=Matrix([[dphidx,dphidy]]) #dphidx y dphidy las hemos calculado en la
#celda de código anterior
print("El vector gradiente de $\phi(x,y)$ es:")
display(gradphi)
Ahora vamos a representar el gradiente (que es un campo vectorial) sobre la representación gráfica del potencial:
L=2 #longitud del dominio
N = 100 #espaciado entre puntos
nq=10
xp = np.linspace(0, L, N) #puntos en x
yp = np.linspace(0, L, N) #puntos en y
X, Y = np.meshgrid(xp, yp) #matriz de puntos
Z = phi(X,Y) #valores de T(x,y) en los puntos
Gx=np.zeros((len(yp),len(xp)))
Gy=np.zeros((len(yp),len(xp)))
for i in range(0,len(xp)):
for j in range(0,len(yp)):
Gx[j][i] = dphidx.subs([(x,xp[i]),(y,yp[j])])
Gy[j][i] = dphidy.subs([(x,xp[i]),(y,yp[j])])
fig, ax = plt.subplots() #genera el objeto "figura"
CS = ax.contourf(X, Y, Z) #hace la representación gráfica
QV = ax.quiver(X[::nq,::nq], Y[::nq,::nq], Gx[::nq,::nq], Gy[::nq,::nq])
#Esto es para configurar ejes, barra de color, etiquetas, etc...
ax.clabel(CS, inline=True, fontsize=10, colors='black')
ax.set_title('Potencial $\phi(x,y)$')
ax.set_xlabel("x")
ax.set_ylabel("y")
fig.colorbar(CS)
Como vemos en la figura anterior, el gradiente muestra la dirección de máxima variación de $\phi(x,y)$.
Derivada direccional. Si queremos calcular la variación de $\phi(x,y)$ en una dirección $\hat{\mathbf{n}}$ cualquiera, lo haremos mediante la derivada direccional, que es el producto escalar:
$$D_{\hat{\mathbf{n}}}\phi(x,y)=\hat{\mathbf{n}}\cdot\nabla \phi(x,y)$$Vamos a calcular la derivada direccional de $\phi(x,y)$ en el punto $(1,0)$ en las direcciones $\hat{\mathbf{n}}_1=(1,0)$, $\hat{\mathbf{n}}_2=(0,1)$ y $\hat{\mathbf{n}}_3=(1/\sqrt{2},1/\sqrt{2})$
#definimos coordenadas del punto
xp=1.0
yp=0.0
#evaluamos el gradiente en el punto (xp,yp) dado
gradphipunto=gradphi.subs([(x,xp),(y,yp)])
print("El gradiente en (1,0) es")
display(gradphipunto)
#definimos el vector n=(1,0)
n1=Matrix([[1,0]])
n2=Matrix([[0,1]])
n3=Matrix([[1/np.sqrt(2),1/np.sqrt(2)]])
#calculamos la derivada direccional
dTn1=n1.dot(gradphipunto)
dTn2=n2.dot(gradphipunto)
dTn3=n3.dot(gradphipunto)
print("\nLa derivada direccional en direccion n1 es:")
print(dTn1)
print("\nLa derivada direccional en direccion n2 es:")
print(dTn2)
print("\nLa derivada direccional en direccion n3 es:")
print(dTn3)
Divergencia y rotacional de un campo vectorial¶
La divergencia de un campo $\vec F$ se calcula como el producto escalar del operador Nabla por el campo, que da lugar a un valor escalar: $$ \nabla \cdot \vec{\mathbf{v}}= \frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}$$
y el rotacional como el producto vectorial del operador Nabla por el campo: $$ \nabla \times \vec{\mathbf{\vec F}}=\begin{bmatrix}{\frac {\partial F_z}{\partial y}}-{\frac {\partial F_y}{\partial z}}\\{\frac {\partial F_x}{\partial z}}-{\frac {\partial F_z}{\partial x}}\\{\frac {\partial F_y}{\partial x}}-{\frac {\partial F_x}{\partial y}}\end{bmatrix} $$
Vamos a trabajar con el siguiente campo vectorial:
$$ \vec{\mathbf{F}}= (2y^2,0,0)$$
y calcular la divergencia y el rotacional:
x,y,z,t=symbols('x y z t')
F=Matrix([[2*sqrt(y),0,0]])
Fx=F[0]
Fy=F[1]
Fz=F[2]
dFxdx = Fx.diff(x)
dFydy = Fy.diff(y)
dFzdz = Fz.diff(z)
divF = dFxdx + dFydy+ dFzdz
print("La divergencia del flujo es",divF)
dFxdy = Fx.diff(y)
dFxdz = Fx.diff(z)
dFydx = Fy.diff(x)
dFydz = Fy.diff(z)
dFzdx = Fz.diff(x)
dFzdy = Fz.diff(y)
rot_x = dFzdy - dFydz
rot_y = dFxdz - dFzdx
rot_z = dFydx - dFxdy
rotF=Matrix([[rot_x,rot_y,rot_z]])
print("El rotacional del flujo es:")
display(simplify(rotF))
Podemos ver que la divergencia cero, pero el campo tiene rotacional distinto de cero.
La representación vectorial del $\nabla \times \vec{\mathbf{\vec F}}$ se puede hacer de la siguiente forma:
L=2 #longitud del dominio
N = 50 #espaciado entre puntos
nq=5
xp = np.linspace(0, L, N) #puntos en x
yp = np.linspace(0, L, N) #puntos en y
X, Y = np.meshgrid(xp, yp) #matriz de puntos
vx=np.zeros((len(yp),len(xp)))
vy=np.zeros((len(yp),len(xp)))
for i in range(0,len(xp)):
for j in range(0,len(yp)):
vx[j][i] = F[0].subs([(x,xp[i]),(y,yp[j])])
vy[j][i] = F[1].subs([(x,xp[i]),(y,yp[j])])
fig, ax = plt.subplots() #genera el objeto "figura"
QV2= ax.quiver(X[::nq,::nq], Y[::nq,::nq], vx[::nq,::nq], vy[::nq,::nq],color="r")
#Esto es para configurar ejes, barra de color, etiquetas, etc...
ax.set_title(r'$\nabla\times\vec{\mathbf{\vec F}}$')
ax.set_xlabel("x")
ax.set_ylabel("y")