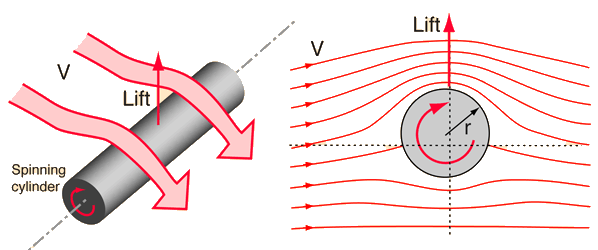
Para representar el campo de velocidades alrededor de un cilindro en rotación podemos utilizar la superposición de tres flujos elementales: un flujo uniforme, un doblete y un vórtice libre, que luego explicaremos en qué consisten. Además, para facilitar el cálculo trabajaremos bajo la hipótesis de flujo ideal. Esto nos permitirá, conociendo el campo de velocidades alrededor del cilindro, calcular la presión en el mismo, para finalmente calcular las fuerzas sobre el cilindro.
A continuación se detallan los flujos elementales mencionados anteriormente:
- Flujo uniforme. Corresponde a una corriente en dirección horizontal con velocidad constante. Su campo de velocidades viene dado por:
$$u_{uniform}\left(x,y\right) = U_{\infty}$$
$$v_{uniform}\left(x,y\right) = 0$$
Doblete. Corresponde a una pareja de fuente y sumidero que se encuentran muy cerca. Su campo de velocidades viene dado por:
$$u_{doublet}\left(x,y\right) = -\frac{\kappa}{2\pi}\frac{x^2-y^2}{\left(x^2+y^2\right)^2}$$
$$v_{doublet}\left(x,y\right) = -\frac{\kappa}{2\pi}\frac{2xy}{\left(x^2+y^2\right)^2}$$
donde $\kappa$ es la intensidad del doblete (a mayor intensidad, mayor será su tamaño y mayores velocidades se alcanzarán en un mismo punto).
Vórtice libre. Corresponde a un flujo en rotación cuya vorticidad es nula (vórtice irrotacional). Su campo de velocidades viene dado por:
$$u_{vortex}\left(x,y\right) = \frac{\Gamma}{2\pi}\frac{y}{x^2+y^2}$$
$$v_{vortex}\left(x,y\right) = -\frac{\Gamma}{2\pi}\frac{x}{x^2+y^2}$$
donde $\Gamma$ es la intensidad del vórtice (a mayor intensidad, mayor velocidad de giro).
Puedes encontrar más información sobre estos flujos elementales en el documento de ayuda.
La superposición de estos tres flujos elementales nos permite representar el flujo alrededor de un cilindro en rotación con el siguiente campo de velocidades:
$$ u=u_{doublet}+u_{vortex}+u_{uniform}$$$$ v=v_{doublet}+v_{vortex}+v_{uniform}$$
En coordenadas polares, este campo de velocidades se expresa como:
$$u_r\left(r,\theta\right) = \cos\theta \left(U_\infty-\frac{\kappa}{2\pi r^2}\right)$$$$u_\theta\left(r,\theta\right) = -\sin\theta \left(U_\infty +\frac{\kappa}{2\pi r^2}\right) - \frac{\Gamma}{2\pi r}$$
Asumiendo que en la superficie del cilindro de radio $R$ la velocidad radial es nula, obtenemos la siguiente expresión para el radio del cilindro:
$$R=\sqrt{\frac{\kappa}{2\pi U_{\infty}}}$$
Por otro lado, también asumiremos la siguiente relación para la velocidad angular del cilindro:
$$\omega=\frac{\Gamma}{2\pi R^2}$$
Sustituyendo las expresiones anteriores, obtenemos:
$$u_r\left(r,\theta\right) = U_\infty \cos\theta \left(1-\frac{R^2}{r^2}\right)$$
$$u_\theta\left(r,\theta\right) = -U_\infty \sin\theta \left(1+\frac{R^2}{r^2}\right) - \frac{\Gamma}{2\pi r}$$
Bajo la hipótesis de flujo ideal, es posible relacionar las condiciones del flujo aguas arriba del cilindro con las condiciones del flujo en cualquier otro punto del dominio mediante la ecuación de Bernoulli:
$$p_\infty + \frac{1}{2}\rho U_\infty^2 = p + \frac{1}{2}\rho U^2$$
Por ejemplo, podemos utilizar esta relación para conocer la distribución de presiones alrededor del cilindro. En el apartado siguiente, representaremos gráficamente el coeficiente de presión, que se define como:
$$C_p = \frac{p-p_\infty}{\frac{1}{2}\rho U_\infty^2}$$
es decir
$$C_p = 1 - \left(\frac{U}{U_\infty}\right)^2$$